Das Verhalten von Flüssigkeiten in dünnen Röhrchen und engen Spalten – Simulation in der Welt der Mikrofluidik und der Kapillaren
Einleitung
Unter Kapillarwirkung versteht man den physikalischen Prozess, bei dem Flüssigkeiten aufgrund der Oberflächenspannung entlang von engen Röhren oder Kapillaren auch gegen die Schwerkraft fließen können.
Die Kapillarwirkung tritt auf, wenn die Adhäsionskräfte zwischen einer Flüssigkeit und der Oberfläche einer festen Röhre stärker sind als die Kohäsionskräfte innerhalb der Flüssigkeit selbst. Je enger der Durchmesser der Kapillare, desto höher kann eine Flüssigkeit in einer Kapillare steigen.
Beispiele für die Kapillarströmung findet man in der Natur, wo Wasser von den Wurzeln der Pflanzen durch feine Kapillaren in den Stängeln und Blättern nach oben transportiert wird. Aber auch die Versorgung des Körpers mit Blut und Sauerstoff wäre ohne die feinen Äderchen, die nicht umsonst Kapillaren genannt werden, ohne Kapillarwirkung nicht denkbar.
Die Kapillarströmung hat praktische Anwendungen in der Technik, wie z.B. in der Mikrofluidik, wo sie zur Kontrolle, Manipulation und den Transport von Flüssigkeiten in winzigen Röhrchen oder Kanälen verwendet wird. Anwendungen gibt es vom Tintenstrahldrucker bis zu medizinischen Diagnosegeräten.
Manchmal ist die Kapillarwirkung auch unerwünscht. In der Bauindustrie kann sie beispielsweise dazu führen, dass Wasser in Beton oder Mauerwerk eindringt und Schäden verursacht. In der Medizin kann sie dazu führen, dass ungewollt Flüssigkeit in Gewebe eindringen kann. Auch in der Mikroelektronik kann die Kapillarwirkung ein Problem darstellen, wenn Flüssigkeiten in die winzigen Lücken zwischen den Chips eindringen und Kurzschlüsse verursachen.
Eine untergeordnete Rolle spielt sie dagegen beim Trinken mit einem Strohhalm. Hier ist der übliche Durchmesser 6 mm. Die Steighöhe beträgt unter der Annahme von Wasser nur 4,64 mm, nicht genug, damit der Cocktail allein in den Mund fließt. Auch ein dünnes Röhrchen hilft wenig, da es sonst zu lange dauert, bis man seinen Cocktail getrunken hat.
Analytische Berechnung
Die Steighöhe einer Flüssigkeit in einer Kapillare kann analytisch mit der sogenannten Jurin-Gleichung berechnet werden. Diese Gleichung beschreibt den Zusammenhang zwischen der Steighöhe einer Flüssigkeit in einer Kapillare und der Oberflächenspannung und dem Durchmesser der Kapillare.
Die Jurin-Gleichung lautet:
h = (2 * γ * cos(θ)) / (ρ * g * r)
Dabei steht
h für die Steighöhe der Flüssigkeit in der Kapillare
γ für die Oberflächenspannung der Flüssigkeit
θ für den Kontaktwinkel zwischen der Flüssigkeit und der Kapillarwand
ρ für die Dichte der Flüssigkeit
g für die Erdbeschleunigung
r für den Radius der Kapillare

Um die Steighöhe h zu berechnen, müssen also die Werte für γ, θ, ρ, g und r bekannt sein. Die Oberflächenspannung γ kann durch ein Oberflächenspannungsmessgerät bestimmt werden. Der Kontaktwinkel θ hängt von der Art der Kapillarwand und der Flüssigkeit und dem gasförmigen Medium ab und kann ebenfalls experimentell ermittelt werden. Die Dichte ρ der Flüssigkeit kann aus Tabellen oder durch Messungen bestimmt werden und die Erdbeschleunigung von g = 9,81 m/s2 ist seit 1686 bekannt, wenn ich mich richtig erinnere.
Die Berechnung der Steighöhe, aber auch der Steiggeschwindigkeit aufgrund der Kapillarwirkung ist in vielen Bereichen von großer Bedeutung, wie zum Beispiel in der Biologie, der Medizin, der Chemie und den Materialwissenschaften. Die Kenntnis der Steighöhe ermöglicht es, Prozesse zu optimieren und Materialien gezielt mit spezifischen Eigenschaften zu entwickeln.
Wie gut ist nun die Simulation bei der Berechnung der Kapillarwirkung?
Hierzu ist im Folgenden ein Benchmark beschrieben, den wir bei Merkle CAE Solutions an einem einfachen Modell mit Star CCM+ nachgerechnet und mit dem analytischen Ergebnis verglichen haben.
Unser Modell besteht aus einem Segment eines Glasröhrchens mit einem Radius von 0,25 mm.

Die Kennwerte für Wasser gegen Luft, die in der Jurin-Gleichung, ebenso wie für das Simulationsmodell in Star CCM+ benötigt werden, sind:
Die Oberflächenspannung Wasser / Luft γ= 0,0728 N/m bei 20 °C.
Der Kontaktwinkel θ Wasser / Luft beträgt etwa θ = 20° bzw. 0,35 rad.
Die Dichte ρ von Wasser beträgt etwa 1000 kg/m3 bei 20 °C.
Die Erdbeschleunigung g beträgt etwa 9,81 m/s2.
Der Radius r = 0,25 mm der Kapillare
Mit diesen Werten kann die Steighöhe von Wasser in einer Kapillare berechnet werden.
Die Jurinformel gibt hier einen Wert von 56 mm an, die CFD-Berechnung bei Merkle CAE Solutions zeigt nach 2 Sekunden einen Wert von 52,5 mm. Die Abweichung beträgt etwa 6%. Der Wert könnte sich aber bei längeren Realzeiten in der Rechnung weiter dem stationären Wert nähern (siehe Abbildung 2).
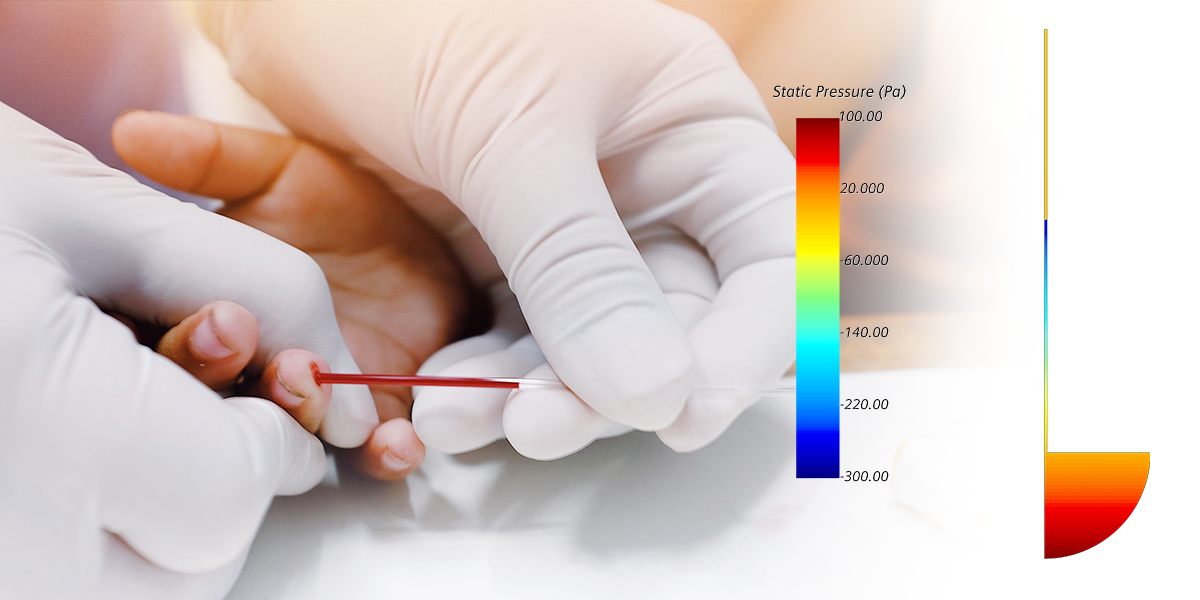
Abbildung 3 zeigt die plausible Oberfläche, den sogenannten Meniskus. Abbildung 4 zeigt die Druckverteilung im Röhrchen.
Nimmt man einen höheren Kontaktwinkel von 60°, werden die Ergebnisse nahezu deckungsgleich (etwa 28 mm). Kein Wunder also, warum Tutorials lieber mit den höheren Werten arbeiten.

Bevor aber hier nun eine Diskussion über die Genauigkeit ausbricht: Es empfiehlt sich auf jeden Fall, das Rechenmodell mit einfachen Versuchen genau für den jeweils vorliegenden Fall abzugleichen. Der Einfluss insbesondere des Kontaktwinkels ist sehr groß.
Auch gibt es im Internet widersprechende Angaben zur Jurin-Gleichung, so ist bei gleichem Formeltyp einmal der Radius r und einmal der Durchmesser d enthalten. Die hier angegebene Formel mit r sollte stimmen.
Der Vorteil der CFD-Simulation mit Merkle CAE Solutions ist, dass die Effekte auch bei sehr komplexer Geometrie abgebildet werden können, bei der die Jurin-Gleichung die Flügel streckt. Zudem können zeitliche Effekte mitberücksichtigt werden, die insbesondere bei schnelleren Taktzeiten von Labormessgeräten eine wesentliche Rolle spielen.

Ihr Stefan Merkle

PS: Bei der Recherche wollte mir Chat GTP glauben machen, dass Insekten aufgrund der Kapillarwirkung mit ihren Füßen trinken. Das konnte ich dann so aber nicht ganz glauben. Vielleicht ist das Wissen vor 2022 hier veraltet und es gibt neue Erkenntnisse… (was ich auch nicht glaube). Vermutlich passt sich Chat GTP der allgemeinen politischen Großwetterlage an, schließlich hat unsere Politik schon länger nichts mehr mit Physik zu tun.
PPS: Quecksilber hat eine sehr hohe Oberflächenspannung mit 484 mN /m und einen Kontaktwinkel von zwischen 135-142 ° gegenüber den meisten Feststoffen. Und tatsächlich ergibt sich eine negative Steighöhe von -25,9 mm bei unserem Trinkhalm. Der Spiegel im Röhrchen liegt also unterhalb der Oberfläche. Schwach kann ich mich an einen Physikversuch in der Schule erinnern, der genau das zeigte. Bleibt nur die Frage, wer Quecksilber mit dem Röhrchen trinken möchte und warum.
PPPS: Maik hat nur Erfahrung mit 40% prozentigen Alkohol-Wassergemischen. Hier ist der Kontaktwinkel nahezu 0, die Oberflächenspannung liegt bei 22,55 mN/m und die Dichte bei 830 kg/m³. Die Steighöhe beträgt dann nur noch 1,84 mm und wird, dem Alkoholkonsum geschuldet, von ihm dann nicht mehr wahrgenommen.






Kommentare und Antworten
Sei der Erste, der kommentiert