Riemenhubtisch

Anhand des Beispiels eines automatischen Parksystems soll aufgezeigt werden, wie sich Mehr- oder Starrkörpersimula-tionen (MKS) zur Lösung von spezifischen kinetischen oder kinematischen Aufgabenstellungen einsetzen lassen. Automatische Parksysteme befördern Fahrzeuge aus der Einfahrtsebene in die verschiedenen Parkebenen. Im hier betrachteten Fall ist das Parkhaus zylindrisch, die Fahrzeuge müssen auf einer Plattform zusätzlich noch gedreht werden, so dass die Palette in den entsprechenden Parkraum geschoben werden kann.
Als Lösungskonzept wurde hier ein sogenannter Riemen-hubtisch verwendet, um die Höhenunterschiede zu überwinden. Der Hubtisch besteht aus zwei Scherenpaaren, die über Rollen-Kurvenscheibenpaarungen bewegt werden können. Der Riemen zieht wie bei einem Seilzug die entlang der Schere verschiebbaren Rollen gegen die Kurvenscheiben und drückt damit die Scheren auseinander. Der Riemen hat eine tragende Funktion. Es muss zum einen ausgeschlossen werden, dass die zulässigen Riemenkräfte überschritten werden, zum anderen darf das Haltemoment des Elektromo-tors nicht überschritten werden, da es sonst zum Kollaps der gesamten Vorrichtung kommt.
Die Berechnungen wurden mit PRO/MECHANICA MOTION durchgeführt. Hierzu wurde die Geometrie der Kurvenscheiben aus vor-handenen CAD-Daten übernommen und das Modell mit der Lage der Gelenkpunkte im ausgefahrenen Zustand als 2D-Modell erstellt. Diese Annahme ist zulässig, da davon ausgegangen werden kann, dass alle vier über der Tischbreite verteilten Riemen gleichmäßig tragen. Die sich ergebenden Kräfte müssen entsprechend umgerechnet werden.

Bild 1 zeigt das MKS-Modell mit Bezeichnung der einzelnen Komponenten. Die Bezeichnung der einzelnen Lager kann aus Bild 2 entnommen werden. Das MKS-Modell und die Annahmen werden im folgenden genauer beschrieben.
MKS-Modell
Da die Kräfte in den Gelenken des Hubtisches und im Riemen in bestimmten Positionen des Tisches stark ansteigen, wurden Überlegungen angestellt, die Gelenke und den Riemen mit Hilfe von pneumatischen Zugzylindern zu entlasten.
Mit Hilfe der Mehrkörpersimulation wurde die Kinematik und der Kraftverlauf im Riemen und in den Gelenkpunkten analysiert und die Lage und die optimalen Kennwerte der Zugzylinder ermittelt.
Die Berechnungen wurden mit PRO/MECHANICA MOTION durchgeführt.
Hierzu wurde die Geometrie der Kurvenscheiben aus vor-handenen CAD-Daten übernommen und das Modell mit der Lage der Gelenkpunkte im ausgefahrenen Zustand als 2D-Modell erstellt.
Diese Annahme ist zulässig, da davon ausgegangen werden kann, dass alle vier über der Tischbreite verteilten Riemen gleichmäßig tragen. Die sich ergebenden Kräfte müssen entsprechend umgerechnet werden.
Bild 1 zeigt das MKS-Modell mit Bezeichnung der einzelnen Komponenten.
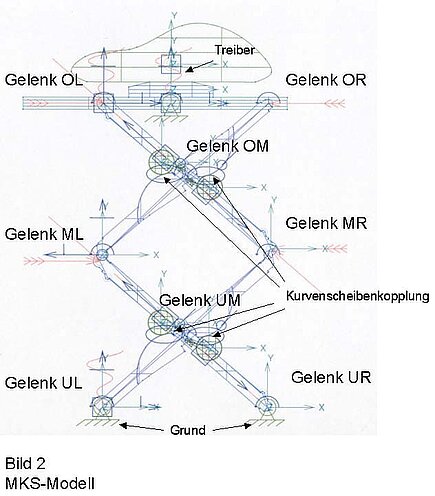
Die Bezeichnung der einzelnen Lager kann aus Bild 2 entnommen werden.
Das MKS-Modell und die Annahmen werden im folgenden genauer beschrieben.

1. Alle Körper [1] werden als starr betrachtet.
2. Die Massen werden im Schwerpunkt der Körper als Punktmassen idealisiert.
3. Die Riemenkraft wird als konstant im gesamten System betrachtet (keine Reibung).
4. Die Umschlingung des Riemens an den Laufkatzen wird mit 180° konstant angenommen (Die Reaktionskraft ist die zweifache Riemenkraft).
5. Die Reaktionskräfte der Riemenumlenkungen werden durch äußere Kräfte berücksichtigt.
6. Alle Gelenke werden als reibungsfrei und ideal betrachtet.
7. Im Modell sind 4 Kurvenscheiben und Rollen enthalten. Die Kurvenscheiben sind mit den von links unten nach rechts oben verlaufenden Scheren fest verbunden. Die Rollen sind entlang der von rechts unten nach links oben verlaufenden Scheren verfahrbar. Zwischen Kurvenscheibe und Rollen wurden reibungsfreie, starre Kopplungen beschrieben, die kein Abheben der Rolle von der Kurvenscheibe erlauben.

8. Zwischen der Basis und dem Oberrahmen wurde ein Antrieb (Treiber) mit einer vorgegebenen, konstanten Geschwindigkeit angesetzt. Als Riemenkraft wird ein empirisch ermittelter Wert angesetzt. Die sich einstellende Restkraft im Antrieb wird gemessen, über bestehende Werte gemittelt und mit der Riemenkraft so verrechnet, dass die Hilfskraft gegen den Wert 0 konvergiert.
9. Der gesamte Verfahrweg des Antriebes beträgt 5160 mm.
10. Der Geschwindigkeitsverlauf beim Anfahren wurde ge-glättet, um das Konvergenzverhalten des Modells zu er-leichtern.
11. Der Gesamthub ist nach 13 Sekunden erreicht (siehe Bild 4).
12. Ausgangsstellung für das Modell ist die obere Stellung.
13. Die Riemenlasten außerhalb der Rollen wurden als äu-ßere Lasten an den Umlenkpunkten angesetzt.
14. Die Lastpfeile mit Federn sind richtungsfest[2], die Lasten ohne Federn sind körperfest[3].
15. Der Kraftbetrag entspricht der im Antrieb ermittelten, zeitlich abhängigen Riemenkraft.
Die Berechnungen erfolgten dynamisch unter Berücksichti-gung der Massenträgheitskräfte durch ein implizites Zeitintegrationsverfahren.
Ergebnisse
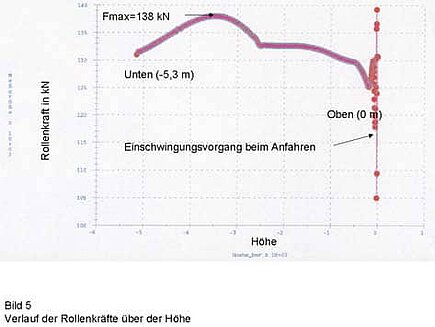
Bild 3 zeigt die beiden Extremstellungen des Hubtisches. Der vorgegebene Verlauf der Höhe über der Zeit ist in Bild 4 dargestellt.
Bild 5 zeigt den Verlauf der Rollenkräfte über der Höhe. Aus dem Verlauf der Kräfte, die im Idealfall konstant sein soll-ten, zeigt sich, das die Kurvenscheiben nicht exakt auf die Kinematik abgestimmt sind. Dies ist darauf zurückzuführen, dass aus Fertigungsgründen eine Form gewählt wurde, die sich aus zwei Kreisbögen zusammensetzt. Am Übergang zwischen den beiden Bögen ist ein Knick im Verlauf der Kräfte zu beobachten (Bild 5).
Beim Anfahren muss das Modell von 0 auf die konstante Verfahrgeschwindigkeit in einem Zeitschritt beschleunigt werden. Dadurch sind die Einschwingvorgänge (bei Höhe 0) zu erklären, die jedoch in Realität so nicht zu erwarten sind, da auch die Beschleunigung des Antriebsmotors endlich ist.

Das Lager MR und die beiden mittleren Lager UM und OM zeigen die höchsten Kräfte, die in der eingefahrenen Stel-lung auftreten (siehe Bild 6). Die Riemenkraft steigt beim eingefahrenen Zustand auf etwa 58 kN an. Da die zulässige Riemenkraft bei 60 kN liegt, besteht hier keine ausreichende Sicherheit mehr, um die Anlage dauerfest zu betreiben. Des weiteren sind die Gelenkkräfte in den Lagern mit 175 bis 180 kN ebenfalls zu hoch, was eine Umkonstruktion der Scheren zur Folge hätte.
Die Idee war, zusätzliche, pneumatische Zugzylinder, die zwischen den Laufkatzen wirken, für eine Entlastung der Gelenke und der Riemen zu sorgen. Problematisch ist in diesem Zusammenhang die Gefahr, dass das Eigengewicht des Hubtisches ohne Fahrzeuggewicht nicht mehr ausreicht, um die Anlage in die unterste Stellung zu fahren.
Mathematisch bedeutet dies, dass die Riemenkräfte negativ werden. Da ein Riemen keine Druckkräfte übertragen kann, wäre die Funktion der Anlage nicht mehr gegeben.
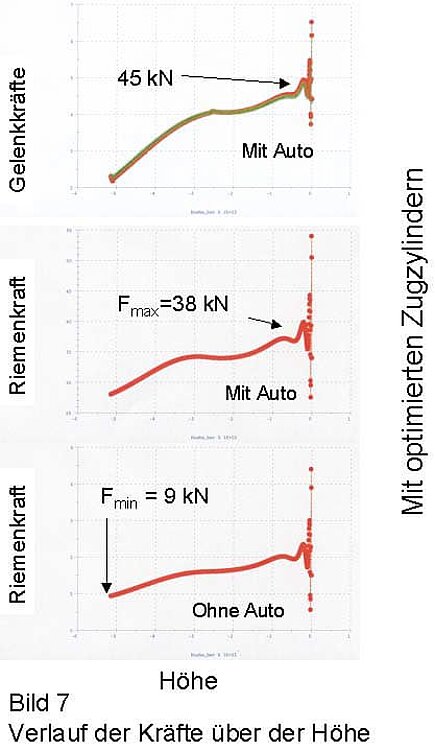
Anhand von mehreren Studien, bei denen die Anlenkpunkte der Zugzylinder und die Federkennlinien variiert wurden, konnte mit Hilfe der Mehrkörpersimulation eine optimierte Konstellation gefunden werden. Die Riemenkräfte konnten im beladenen Zustand auf 38 kN gesenkt werden und die minimale Riemenkräfte sind ohne Beladung mit 9 kN noch ausreichend groß genug.
Die maximalen Gelenkkräfte reduzierten sich von 180 kN auf 45 kN. Somit konnte mit einem vertretbaren Aufwand die Sicherheit der Anlage gewährleistet werden, ohne die Funktion einzuschränken.
Die Mehrkörpersimulation erwies sich bei der Simulation des Hubtisches als ein geeignetes Instrument, die Kinematik besser zu verstehen, kritische Zonen zu finden und geeignete Maßnahmen zur Optimierung abzuleiten.
[1]Körper: In diesem Zusammenhang jede Einheit, die für sich betrachtet als starr angesehen kann und über sogenannte Gelenke mit anderen Körpern kinematisch verbunden ist.
[2] Richtungsfest: Die Orientierung des Lastvektors im globalen Koordinatensystem bleibt gleich.
[3] Körperfest: Die Orientierung des Lastvektors im lokalen Koordinatensystem des Körpers bleibt gleich. Hier: Die Lastrichtung wirkt immer in Richtung der Schere.