Warum ein Fehler von 1.000 % manchmal gar nicht schlecht ist

Betrachten wir einen einfachen Zugversuch einer metallischen Probe. Aufgenommen wird die Kraft-Wegkurve einer Probe. Bis zum Erreichen der Dehngrenze ist der Anstieg linear. Bei einer Erhöhung der Kraft treten zusätzlich plastische Dehnungen auf, die nicht mehr zurückgehen.

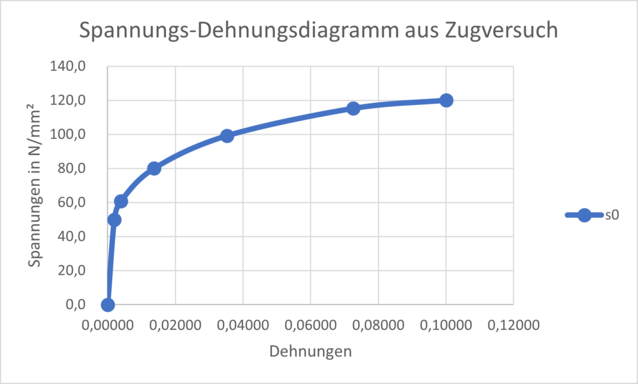
Bezieht man die Kraft auf den Anfangsquerschnitt der Probe und die Verschiebung auf die Länge der Probe, kommt man zum sogenannten technischen Spannungs-Dehnungsdiagramm (siehe Abbildung 1).

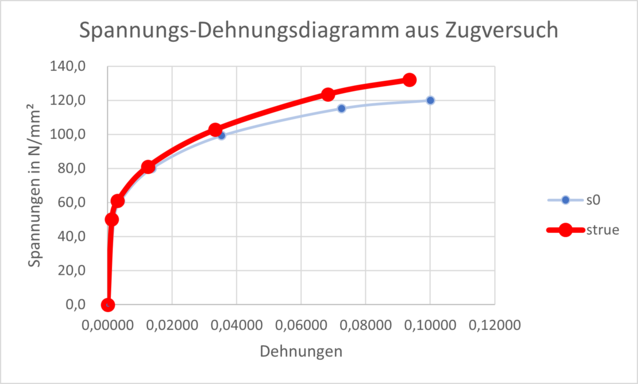
Da sich der Querschnitt der Probe durch Einschnürung aber ändert, kann man unter der Annahme, dass das Volumen gleichbleibt, die sogenannten „Wahren Spannungen und Dehnungen“ bestimmen, die man üblicherweise als Werkstoffdaten in einer Finite-Elemente-Berechnung FEM benutzt.

Da die wahren Spannungen immer größer sind als die Technischen, kann man der Einfachheit halber auch die technischen Werte ansetzen (ein paar Schritte zur sicheren Seite des Abgrunds nach rechts).

Machen wir ein einfaches Beispiel:

Für einen Aluminiumwerkstoff finden wir die Angaben:

Dehngrenze        Rp0,2     = 50 N/mm²
Zugfestigkeit        Rm        = 120 N/mm²
Bruchdehnung     A5        = 10 %
E-Modul               E          = 70.000 N/mm²

Hier handelt es sich um die technischen Kennwerte.

Mit diesen Werten können wir bei Merkle CAE Solutions schon grob das plastische Materialverhalten beschreiben, falls die genaueren Werte des Zugversuches (siehe Abbildung 2) nicht vorliegen.

Eine Umrechnung in die wahren Spannungen und Dehnungen ergibt:

Dehngrenze        Rp0,2     = 50,1 N/mm²
Zugfestigkeit        Rm        = 132 N/mm²
Bruchdehnung     A5        = 9,12 %
E-Modul               E          = 70.000 N/mm²

Hier zeigt sich, dass die Dehngrenze und die Zugfestigkeit etwas steigen, während die Bruchdehnung etwas abnimmt. Bei kleineren Dehnungen sind die Kurven aber nahezu deckungsgleich.

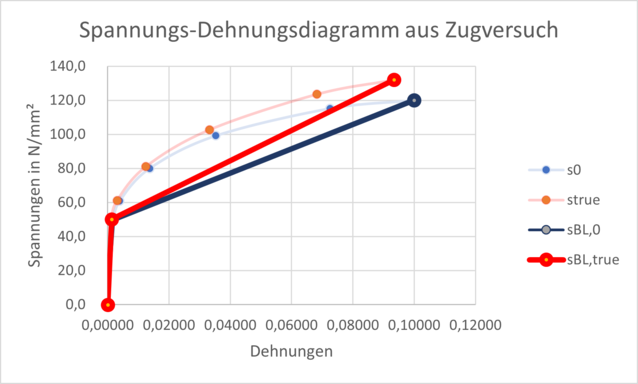
Charakterisiert werden kann das plastische Verhalten auch durch zwei Geraden. Man spricht hier von einem bilinearen Materialmodell. Dies hat den Charme, dass sich die Werte dazu direkt aus einem Tabellenbuch entnehmen lassen (Abbildung 3).

Wenn man sich die Rechnerei schenken möchte und lieber noch einen Schritt weiter nach rechts gehen möchte, kann man statt den wahren (rote Kurve) die technischen Werte (blaue Kurve) für die Berechnung nehmen. Es ergeben sich dann bei einer bestimmten Spannung immer höhere Dehnungen.

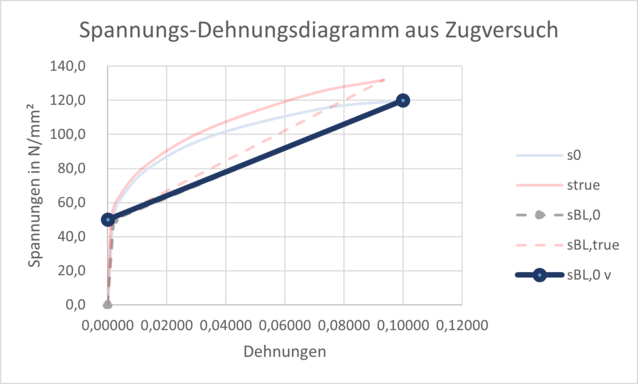
Aber es geht noch einfacher: Die elastischen Dehnungen bei der Dehngrenze Rp0,2 (0,2% plastische Dehnungen = 0,002) sind im Low Cycle Fatigue sehr viel kleiner als die tatsächlichen plastischen Dehnungen, die im Bereich von vielleicht 1-5% liegen.

Die Kurve unterscheidet sich nicht sichtbar vom bilinearen Gesetz und ist denkbar einfach: Schnittpunkt zur y-Achse ist die Dehngrenze und der zweite Punkt ist die Zugfestigkeit bei der Bruchdehnung (siehe Abbildung 4).

Über eine Finite-Elemente-Berechnung können wir bei Merkle CAE Solutions an einem Bauteil mehrere Belastungszyklen rechnen und den Verlauf der Summe der inkrementellen plastischen Dehnungen durch eine geeignete Funktion abschätzen. Steigt die Differenz von Zyklus zu Zyklus an, ist die Funktion eine e-Funktion, bleibt sie konstant, ergibt sich eine lineare Funktion, sinkt sie, ergibt sich eine logarithmische Funktion.

Bei thermisch stark beanspruchten Anlagen, wie Abgasanlagen und Kühlern, wird man feststellen, dass sich in der Regel logarithmische Funktionen ergeben. Kennt man den voraussichtlichen Funktionstyp, reicht bereits ein gerechneter Zyklus, um die ertragbare Lastspielzahl abschätzen zu können.

Abbildung 5 zeigt die ertragbaren Lastwechsel bei zwei plastischen Dehnungen. Gehen wir davon aus, dass wir im Modell mit den oben angenommenen Werkstoffkennwerten eine ertragbare Lastspielzahl von 150 Lastwechseln (e=1,2%) errechnet haben. Der Versuch zeigte aber, dass ein Ausfall erst bei 1.500 Lastwechseln (e=0,865%) auftrat.

Jetzt stellt sich die Frage, um wieviel höher die Dehngrenze des Werkstoffs sein müsste, damit Versuch und Rechnung übereinstimmen.

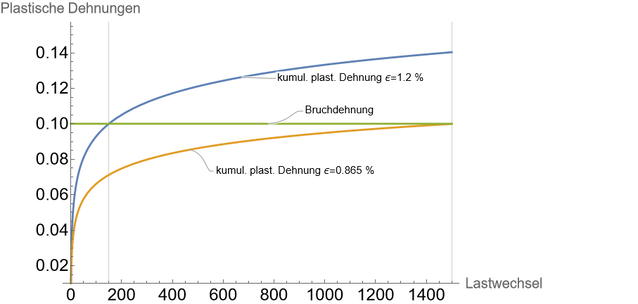
Die Antwort gibt uns das vereinfachte Materialmodell in Abbildung 6:

Um von einer plastischen Dehnung von rd. 1,2% auf 0,865 % zu kommen, ist es rechnerisch ausreichend, im Materialmodell die Dehngrenze von 50 N/mm² auf 52 N/mm² zu erhöhen.

Da Materialkennwerte im Regelfall Mindestwerte darstellen, die mehreren Prozent Streubreite haben, ist allein hieraus der Unterschied in der Lebensdauer rechnerisch erklärbar. Ein weiterer Effekt, der zu einer höheren Dehngrenze führt, ist die zyklische Verfestigung eines Werkstoffs, die mangels entsprechender Daten meistens vernachlässigt wird.

Allein eine höhere Dehngrenze, in diesem Fall von 4% von 50 auf 52 N/mm², ist ausreichend, um die Diskrepanz von 150 Lastwechseln zu 1.500 Lastwechseln zu erklären. Die gemessene Streckgrenze einer Charge liegt oft weit mehr als 4% über der angegebenen Mindeststreckgrenze.